Photon Mapping Superluminal Particles

Abstract

One type of light source that remains largely unexplored in the field of light transport rendering is the light generated by superluminal particles, a phenomenon more commonly known as Cherenkov radiation [Cherenkov1937]. By re-purposing the Frank-Tamm equation [Frank1991] for rendering, the energy output of these particles can be estimated and consequently mapped to photons, making it possible to visualize the brilliant blue light characteristic of the effect. In this paper we extend a stochastic progressive photon mapper and simulate the emission of superluminal particles from a source object close to a medium with a high index of refraction. In practice, the source is treated as a new kind of light source, allowing us to efficiently reuse existing photon mapping methods. <ccs2012> <concept> <concept_id>10010147.10010371.10010372.10010374</concept_id> <concept_desc>Computing methodologies Ray tracing</concept_desc> <concept_significance>500</concept_significance> </concept> </ccs2012>

[500]Computing methodologies Ray tracing

1 Introduction

In the late 19th and early 20th century, the phenomenon today known as Cherenkov radiation were predicted and observed a number of times [Watson2011] but it was first properly investigated in 1934 by Pavel Cherenkov under the supervision of Sergey Vavilov at the Lebedev Institute [Cherenkov1937]. A few years later, Cherenkov’s colleagues Igor Tamm and Ilya Frank developed the theory for the effect in 1937 within the framework of Einstein’s special relativity, effectively summarizing the phenomenon in the so-called Frank-Tamm equation [Frank1991].

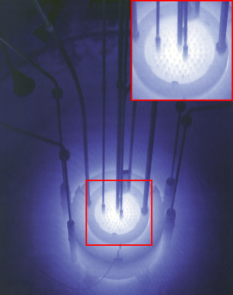
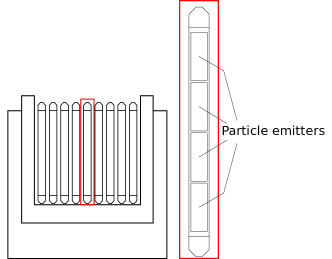
Normally, the phenomenon is observed in nuclear reactors or in the proximity of highly radioactive materials, see e.g., figure 6. Thus, the effect can also be used in the reverse order: the detected light from the Cherenkov effect can give a hint about the remaining radioactivity of the substance. For this reason, the effect is often used in detectors for radioactive substances [Watson2011]. Additionally, there is an increasing number of attempts to use the phenomenon in the field of medicine, either as a complement to other methods or as a completely novel imaging technique for in vivo imaging [Ciarrocchi2017].

1.1 Cherenkov Radiation

Physically, as a charged particle (e.g., an electron) moves through a medium it will interact with the particles of that medium, temporarily exciting its electrons and causing them to emit electromagnetic waves moving at the speed of light for the current medium (formally this is referred to as the phase speed of the medium). According to Huygen’s principle, these waves travel outwards spherically from the point interaction. Normally, these spheres will accumulate in the direction of the particle but will not otherwise cross one another, as depicted in figure 1. However, if the particle travels faster than these spheres the waves will constructively interfere, generating coherent photons at an angle proportional to the velocity of the particle, similar to the propagation of a sonic boom from supersonic aircraft.

Figure 1: Schematic view of the creation of Cherenkov photons where $c_m$ represents the speed of light in the medium and $v_p$ is the speed of the particle. Structurally, this is similar to a sonic boom for sound waves.

Formally, this occurs when the criterion is fulfilled, where $c_0$ is the speed of light in vacuum and $n$ is the refractive index of the medium. That is, Cherenkov radiation occurs when the particle travels faster than light inside the current medium. Additionally, the angle at which the coherent photons are emitted can be computed from figure 2 using trigonometry:

$$cos(\theta )=\frac{c_0}{v_{p}n}$$

Figure 2: The angle at which Cherenkov radiation will be emitted at each unit distance. Note that the particle in this figure is significantly faster than the other ones to better illustrate the concept.

1.2 The Frank-Tamm Equation

The Frank-Tamm equation [Frank1991] describes how the photon energy gets distributed by charged particles that travel faster than the speed of light in the current medium. Typically, it is given in the form:

$$\frac{d^{2}E}{dxd\omega }=\frac{q^2}{4\pi }\mu (\omega )\omega \left(1-\frac{c_0^2}{v^2{n}^2(\omega )}\right)$$ (1)

Where:

$\omega$

Is the angular frequency of the photon.

$\mu (\omega )$

The permeability of the medium.

$q$

The electric charge of the particle.

$n(\omega )$

The refractive index of the medium.

$v$

The speed of the particle.

$c_0$

The speed of light in a vacuum.

$\frac{d^{2}E}{dxd\omega }$

Energy emitted per unit length $x$ traveled and frequency $\omega$.

For our purposes, it is more practical to use wavelengths ($\lambda$) and number of emitted photons ($N$). Thus, the equation is rewritten to the following:

$$\frac{d^{2}N}{dxd\lambda }=-\frac{2\pi \alpha \mu (\lambda )}{{\lambda }^2}\left(1-\frac{c_0^2}{v^2{n}^2(\lambda )}\right)$$ (2)

Where $\alpha$ is the free structure constant.

If we additionally assume that $\mu (\lambda )\approx 1$ the Cherenkov radiation spectra is straight-forward to visualize, as shown in figure 3.

Figure 3: Example of how equation 2 maps particle energy to photons. Depicted here for an electron moving through heavy water ($n\approx 1.328$) at a speed of $0.8c_0$, assuming that $\mu (\lambda )=1$.

Note how the curve rises rapidly for shorter wavelengths and especially in the ultraviolet range which is one of the reasons that give Cherenkov its brilliant blue glow. As given, this equation would simply continue to rise for shorter and shorter wavelengths but in the region of anomalous dispersion the refractive index drops below unity, effectively stopping the effect. Similarly, at longer wavelengths in the infrared spectra and beyond, the effect stops due to material self-absorption [Ciarrocchi2017].

2 Related Work

While the Cherenkov effect is a widely understood physical phenomenon with various avenues of active research within medicine [Ciarrocchi2017], nuclear physics and astronomy. To our knowledge, the effect has not been studied in a ray tracing or computer graphics context. That said, there exists a few frameworks for simulating the Cherenkov effect such as Geant4, but to our knowledge, they are not based on ray tracing techniques. Additionally, a few other phenomena involving charged particles have been studied within this context, one of which being the rendering of the formation of auroras [lawlor2011], but they are fundamentally different from the effect discussed here.

3 Photon Mapping Algorithm

The idea is to extend the progressive photon mapping algorithm [hachisuka2008] with an additional pass: Trace $M$ charged particles from predetermined sources in the scene and store the path that they traveled. This paper modifies a traditional photon mapping algorithm to use particle paths as light sources that can be fed into the remaining passes of the algorithm with a different sampling strategy:

1. Randomly choose a point along the path that the charged particle traveled.

2. Determine the index of refraction at the location.

3. If the particle is not superluminal at that point, emit a photon in a random direction.

4. Otherwise, compute the Cherenkov emission angle (see figure 2) and randomly choose a direction perpendicular to the cone surface to emit a photon towards.

5. Evaluate the Frank-Tamm equation for the particle and use the resulting spectra as photon color.

6. Trace the photon as in [hachisuka2008].

Intuitively, the algorithm can be summarized as follows: As a charged particle travels through matter, it will excite the atoms of the material causing it to emit photons uniformly in a sphere. However, if the particle is in a medium where it is superluminal the photons will instead constructively interfere and primarily be emitted in the cone defined by the Cherenkov angle. The sampling scheme is also summarized in figure 4.

Figure 4: Illustration of how uniform random variables are used to generate new photons. $u_0$ selects a point along the particle path, $u_1$ retrieves a value on the disk defined by the cherenkov angle.

3.1 Photon Density Distributions

Photon mapping is a Monte Carlo simulation and as such, it is often desirable to use statistical Russian roulette to improve rendering performance. To do so however, the photon probability density function $p(\text{o},\omega )$ must be estimated. Given the particle light source defined by our algorithm, it can be derived as follows:

$$p(\text{o},\omega )=p(\text{o})\cdot p(\omega )$$

Where $p(\text{o})$ and $p(\omega )$ are the density for the photon origin and direction respectively. Of these, $p(\text{o})$ is straightforward to compute: The particle origin will always be somewhere along the path of the particle, hence the density is simply:

$$p(\text{o})=\frac{1}{\text{total particle length}}$$

As the ray direction in our algorithm can be either uniformly distributed on a sphere or along the Cherenkov angle, $p(\omega )$ is slightly trickier to estimate. To do so, we first define a probability mixture model as follows:

$$p(\omega )=p(S)p({\omega }_{\text{c}})+(1-p(S))p({\omega }_{\text{s}})$$

Where $p(S)$ is the probability of the particle being superluminal and $p({\omega }_{\text{c}})$ and $p({\omega }_{\text{s}})$ are the probability densities of emitting light along the Cherenkov angle and uniformly in a sphere respectively. As $p({\omega }_{\text{c}})$ and $p({\omega }_{\text{s}})$ are well known, this can be reduced to:

$p(\omega )$ $=p(S)p({\omega }_{\text{c}})+(1-p(S))p({\omega }_{\text{s}})$

$={\displaystyle \frac{p(S)}{2\pi }}+{\displaystyle \frac{1-p(S)}{4\pi }}={\displaystyle \frac{1+p(S)}{4\pi }}$

Also, if it is possible to find all intervals where a particle is superluminal, $p(S)$ can be estimated as:

$$p(S)=\frac{\text{superluminal path lengths}}{\text{total path length}}$$

4 Results

The algorithm itself is implemented as a new kind of light source in the ray tracing framework PBRT [PBRT3e], the code of which will be made available on GitHub. Note that no other part of the framework had to be changed to add this feature.

To demonstrate the effect in a simple setting, a variant of the Cornell box is used where at least one of the objects emits charged particles. Additionally, as Cherenkov radiation is most commonly observed in the context of nuclear reactions, an additional scene of a nuclear reactor is created based on photographs of the Reed Research Reactor. By replicating the phenomenon in such a setting the output image from the photon mapper will be comparable to photographs of the same reactor when it is in operation. The resulting images from these scenes can be seen in figures 5 and 6.

5 Discussion

The Cornell box scenes clearly visualizes the cone shape of the emitted Cherenkov photons and how they are affected by varying refractive indices. Further, the Reed model shows how the sheer mass of photons eventually diffuses to something akin to a single source of light. Naturally though, the render differs from the photograph but that is to be expected for a number of reasons, chief of which is the inability to closely model particle absorption properties in the scene.

Note that the brilliant blue light that Cherenkov radiation creates can be faked using conventional virtual light-sources, but as we demonstrated with PBRT the effect can be implemented succinctly as a custom light-source without changing the ray tracer itself. Furthermore, there may be cases where simulating the effect might be useful, such as generating reference images that artists can base their work on. Additionally, this kind of simulation could be used as a reference for how a reactor vessel should look like during operation, prior to it even being built. Further, since the phenomenon is utilized in detectors, this kind of simulation could give an idea of where such devices should be placed in a reactor environment.

5.1 Future Work

In this work, it was assumed that the emitted particles traveled in straight lines similar to normal rays. In reality, particles interact with matter to a larger degree and often change propagation direction afterwards. Thus it may be of interest to model the particle path as more of a random walk instead. It is also worth noting that the current algorithm only works for forward and bidirectional ray tracers. It is not clear how this kind of light source would be sampled in backward rendering frameworks, such as those based on path tracing [Kajiya1986]. Also, this work primarily focused on surface photon-mapping but as Cherenkov radiation is normally seen as a volumetric effect it should be analyzed in a setting where this can be taken into account, such as in [vpm1998], [jarosz11] or [novak12vrls]. Additionally, the passage of a charged particle is an inherently transient event. For this reason, it may be interesting to integrate the effect in a transient photon rendering framework, such as the one described by [MarcoCGF2019PTPB].

6 Conclusions

This paper describes an extension to the stochastic progressive photon mapper algorithm [hachisuka2008] which allows it to visualize a phenomenon from nuclear physics that typically only occurs under specific conditions, namely the Cherenkov effect. We implemented the effect in an existing physically based rendering framework (PBRT), which produced the expected results. It also shows that similar ray tracing techniques may be applicable to other phenomena from nuclear physics. Additionally, with increasing focus on using the Cherenkov in medicine it may be of interest to use ray tracing algorithms to accelerate their applications or improve their methods.

6.1 Acknowledgments

This work was partially supported by the Wallenberg AI, Autonomous Systems and Software Program (WASP) funded by the Knut and Alice Wallenberg Foundation. We would also like to thank Arm Sweden AB for letting Gustaf pursue a PhD as one of their employees. Additionally, we would like to thank Pierre Moreau and Simone Pellegrini for their valuable input during this work.

Figure 5: Schematic and renderings of the Cornell box. From left to right: (a) Schematic drawing with the particle and Cherenkov angle highlighted. (b) Schematic with a particle source emitting uniformly from a small cylinder in the box center towards cylinders with varying refractive indices. (c, d) Rendering of (a) and (b) respectively.

Figure 6: From left to right: (a) A photograph of the Reed research reactor. (b) Rendering of a reactor model based on the Reed reactor using our algorithm with a large number of particle emitters. Note how the large amount of Cherenkov radiation coalesce into something resembling a single light source. (c) Schematic of the reactor interior and particle emitter structure in the model.