Succinct Opacity Micromaps
Abstract.
Alpha masked geometry such as foliage has long been one of the trickier things to render efficiently, both for rasterization based approaches and for hardware accelerated ray-tracing. Recently, a new type of primitive was introduced to the Vulkan® and DirectX® ray-tracing APIs that promises to alleviate this issue: Opacity Micromaps, a structure that uses a bit of extra memory as hints to the pipeline when it should actually call the AnyHit-shader. In this paper, we extend this primitive with a novel compression method that uses the concept of succinct 4-way trees to reduce the memory footprint by up to times, including an algorithm for looking up micromap values directly from this compressed form. Further, we perform a comprehensive analysis of the generated micromaps to demonstrate their performance in terms of both memory footprint and frame render time compared to a number of similar structures. Finally, we highlight some aspects of the extension that developers and artists should be aware of to make the most out of it.

1. Introduction
Transparency has always been a challenging effect to apply for computer graphics systems. Particularly for rasterization based methods that frequently have to resort to various tricks to ensure that the effect looks correct (McGuire and Mara, 2017). In contrast, the linear propagation of rays simplifies this matter for ray-tracing methods, typically removing the need for these tricks. Thus, with the advancement in hardware accelerated ray-tracing methods, the hope has been that transparency effects would become much more prevalent. This has not materialized in practice, in part due to the remaining dependence on the rasterization pipeline in many frameworks, but also due to the so called AnyHit-shader (Werness, 2023) that must be invoked to correctly apply most transparency effects. As this shader is situated in one of the innermost loops of the ray-tracing pipeline it has ended up as a major bottleneck for these effects.
Recently, there has been an effort to improve this matter for one particular transparency effect: Alpha masked geometry, which is frequently used on foliage, leaves and branches in many scenes. This is done by introducing a new kind of abstraction known as an opacity micromap that encodes a limited amount of transparency information on a subsection of each triangle and allows this information to be quickly accessed with the ray-triangle intersection data, without having to load any other metadata. And most crucially, without having to call the AnyHit-shader during the traversal or even interrupt the hardware traversal (Sjöholm, 2022), thus promising an improved ray-tracing performance for these effects.
2. Related Work
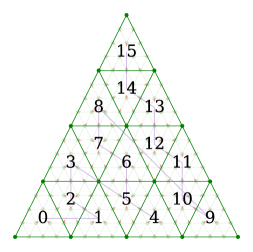
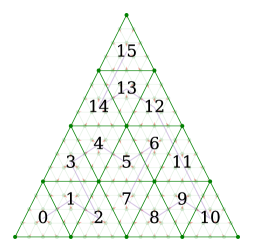
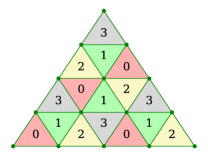
The concept of micromaps were first presented by (Gruen et al., 2020): A relatively simple format that divided a triangle into a regular grid with a simple indexing algorithm. This basic concept has remained in the current Vulkan® and DirectX® extension, but the subdivision scheme has been changed as shown in figure 2 and discussed further in Section 4.3.
Further, (Fenney and Ozkan, 2023) were first to present a scheme for compressing a two-dimensional single channel opacity map to the same states as the micromap presented by Gruen et al.. This scheme compresses the maps very well (down to between of the original size), but are fundamentally different from the final micromaps in use by Vulkan® and DirectX®. A direct comparison to our work is difficult to accomplish for two reasons: (1) Their methods are not directly available in any Graphics API, and (2) the encoding scheme uses assets with quads in a way that is not widely used in practice. Interestingly, Fenney and Ozkan also mention investigating an explicit 3-level quad-tree method as well as a wavelet mod 3 scheme. However, no details regarding this investigation was included in their work.
Coincidentally, work related to compressing displacement data into micromaps are covered by (Maggiordomo et al., 2023). Notably, this type of micromap is primarily used to reduce the footprint of displacement data rather than to provide any frame-time improvement. However, as this work is not related to opacity micromaps, it will not be covered by this paper.
3. Background
This section provides a general background to the technologies used to develop our algorithms.
3.1. Micromaps
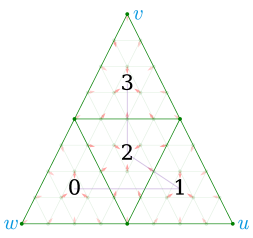
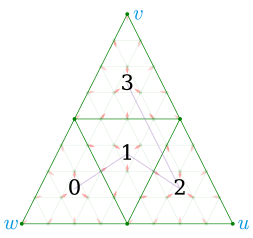
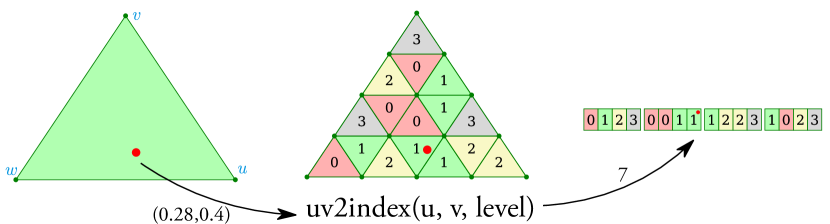
In brief, a micromap is simply a linear array of values mapped into fixed sub-areas of a triangle specified by a space-filling curve as shown in figures 2 and 3. To date, there are only two kinds of official micromaps:
-
•
Opacity Micromaps (OMM), and
-
•
Displacement Micromaps (DMM).
Of these, only the opacity micromaps is currently available as a generally available Vulkan® and DirectX® extension (Werness, 2022). Further, an opacity micromaps can only contain a very specific set of opacity values depending on whether it is operating in the so-called 2-state or 4-state mode:
| 2-State | 4-State | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
As these values only occupy either 1 or 2 bits each, the opacity micromap is typically handled as a type of bit-vector. Functionally, the values are mostly self-explanatory:
-
•
Fully transparent and opaque means that that particular sub-triangle is either completely opaque or transparent.
-
•
Unknown values should look up the actual opacity values using some other method, by e.g., looking it up in an alpha texture. Additionally, these values can be converted to an equivalent 2-state value, e.g., when it is undesirable to perform the alpha texture lookup, such as for shadow-rays in the ray-tracing pipeline.
Thus, this extension is primarily aimed at improving the rendering performance of alpha mapped geometry, such as foliage for the DirectX® and Vulkan® ray-tracing and ray-query extensions by avoiding most, if not all, AnyHit calls or returns to the calling shader. A case where ray-tracing has long promised to excel over rasterization based methods, but failed in practice, primarily due to having to call the AnyHit-shader inside the ray-tracing traversal pipeline.
Opacity micromaps are intended to solve this: Provide a relatively small amount of extra data with hints to the ray-tracing pipeline when to avoid calling the AnyHit-shader, and consequently reduce the overall texture and memory bandwidth. However, these optimizations are entirely in the hands of the users: It is up to them to generate appropriate micromaps and apply them correctly to see any appreciable improvements.
3.1.1. Highest Useful Subdivision Level
In 4-state mode, the subdivision level is typically only another tool to dial in performance, effectively trading runtime at the expense of memory. In 2-state mode, the triangle shape and subdivision level directly influence the final geometry as there are no unknown values, and consequently no way of calling an AnyHit-shader. This shape may be distinctive, especially compared to low resolution alpha texels, as seen in figures 1 and 6. Thus, if the intent is to conservatively recreate the alpha texture with micromaps, it is useful to estimate the maximum useful subdivision level by computing when the texture coordinate length of a subtriangle along the longest edge is less than one pixel, i.e., when the subtriangles are smaller than the pixels. In other words:
| (1) |
This is valid regardless of any minification or magnification issues introduced by camera motion as long as the texture coordinates are static. However, this becomes more complicated for primitives with coordinate transforms, but if it is possible to estimate the maximum deformation, the same approach can still be used.
3.1.2. Special Indices
In Vulkan®, Opacity micromaps are applied on triangles by providing an array of so-called triangle indices at the creation of a bottom level acceleration structure (BLAS). However, it is relatively common for micromaps to contain only a single value, which may be wasteful, especially at high subdivision levels. To alleviate this, Vulkan® provides a set of special index values to map directly to these cases:
| -1 | VK_OPACITY_MICROMAP_SPECIAL_INDEX_FULLY_TRANSPARENT_EXT |
| -2 | VK_OPACITY_MICROMAP_SPECIAL_INDEX_FULLY_OPAQUE_EXT |
| -3 | VK_OPACITY_MICROMAP_SPECIAL_INDEX_FULLY_UNKNOWN_TRANSPARENT_EXT |
| -4 | VK_OPACITY_MICROMAP_SPECIAL_INDEX_FULLY_UNKNOWN_OPAQUE_EXT |
These values can be used in some cases to reduce bandwidth or otherwise simplify the micromap processing.
3.2. Succinct Data Structures
One type of data structure that is not widely used throughout the field of computer graphics is the so-called succinct data structure, originally introduced by (Jacobson, 1989). These types of data structure are so called because of their small memory footprint: Typically only a constant factor from the information-theoretical minimum.
As a concrete example, consider all binary trees with nodes. There are only a finite number of these trees, given by the Catalan number ([)A000108]oeis. As such, there are approximately distinct trees for large values of . Consequently, it is possible to enumerate them and encode the trees using only bits.
Depending on the desired properties, a number of different encoding schemes could be used: The simplest of which is to perform a depth-first search over the tree, setting a bit to if the node is an internal node and otherwise. Thus representing the entire tree and allowing us to readily count the number of internal and leaf nodes in the tree using population counts on the bits themselves. Further, these counts can be used as indices for retrieving data stored in the abstract tree nodes.
4. Algorithms
In this section we will present the primary algorithmic contributions of this paper.
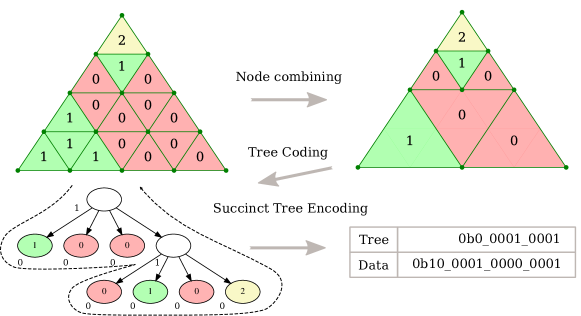
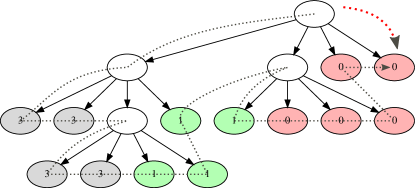
4.1. Succinct Tree Encoding
There are quite a few ways of encoding an existing micromap as a succinct tree, but one of the simplest can be expressed as follows:
-
•
Construct the perfect 4-way tree from the flat micromap from the bottom up by merging adjacent nodes with identical values (algorithm 1), then
-
•
encode the resulting perfect tree as a succinct tree (algorithm 2).
An example of this is illustrated in figure 4.
4.2. Succinct Tree Decoding
Given an encoded tree, it is straightforward to convert this back to a non-encoded tree, and by extension, the original micromap. It is however also possible to traverse this bit-vector to directly access the underlying micromap value. This can be done with algorithm 3. Note that the algorithm is strongly tied to the bit-representation of the tree. If the representation is changed, the algorithm must change accordingly.
4.3. Micromap Indexing
The Vulkan® micromap extension includes an algorithm for converting barycentric coordinates to an index into the micromap structure, in this paper referred to as the reference algorithm (Werness, 2022). However, this algorithm is arguably not very easy to understand due to the opaque nature of the numerous bit-wise operations. To that end, we devised an arguably simpler, iterative algorithm (4), that to our knowledge, has not been published elsewhere yet. In brief, it does the following:
-
•
Explicitly compute all barycentric coordinates for the hit point, then use these to determine which of the 4 sub-triangles (eft, iddle, ight or op) is hit by the intersection.
-
•
Increment the index and recompute the barycentric coordinates according to the intersected subtriangle.
-
•
Recurse until the desired subdivison level is reached.
Note that the majority of the conditions and their ordering is done to correspond exactly with the reference algorithm, as it has some peculiar rounding behavior in the edge and corner cases, as shown in figure 2. Moreover, a detailed description of this algorithm and how the expressions were derived can be found in Appendix A. Additionally, this new algorithm has been proven to be equivalent to the reference up to subdivision level using the ACL2 theorem prover (Kaufmann and Moore, 2004) using rational numbers. It is not clear whether the discrepancy at level 16 is an error in our algorithm, a failure in the reference due to an overflow condition or some kind of floating point issue. However, it is obvious that the reference algorithm must be rewritten to handle more than 16 subdivision levels as the final interleaving step cannot handle more than 16-bit values. Although, a micromap of that size () appears to be of little practical use at this time.
5. Results
The evaluation of the algorithms is split into two parts: One representing the compression potential of the succinct tree encoding, the other, the frame rendertime. In both cases, the algorithms are tested on the scenes described in table 1. Opacity micromaps are generated from the original alpha masks up to subdivision level 6, all of which can be found in the supplemental material. In total, we evaluate six different methods:
- Micromap:
-
Micromaps emulated in software.
- Tree:
-
Tree encoded micromaps.
- Vulkan Fast-Build (FB):
-
Vulkan Micromaps built with the Fast-Build flag.
- Vulkan Fast-Trace (FT):
-
Vulkan Micromaps built with the Fast-Trace flag.
- Bitmask:
-
A pseudo-texture where every 1 or 2 bits represent the alpha value.
- Texture:
-
The original alpha texture.
Every method except the texturing approach can also run in either 2-state or 4-state mode as described in Section 3.1.
5.1. Compression
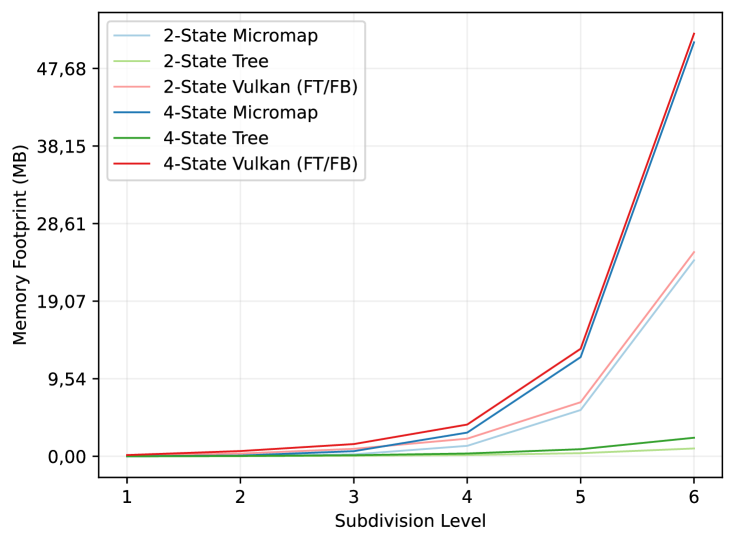
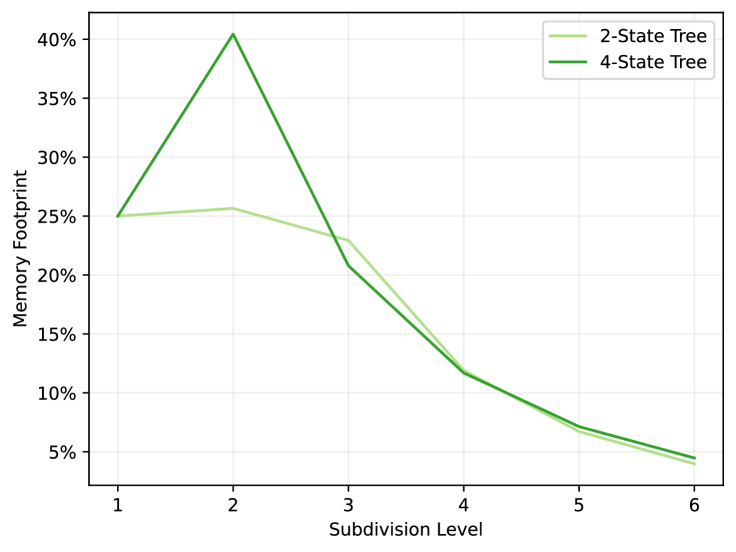
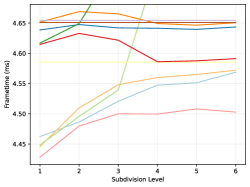
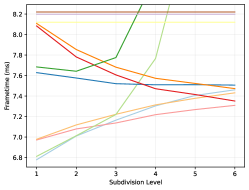
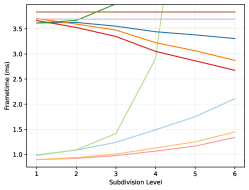
We evaluate each opacity method by estimating their total memory footprint. For micromap approaches, this includes the micromap data itself, the so-called triangle indices, and any metadata structure. Only the micromap data is included for the Vulkan methods however, as they may embed any additional metadata in the acceleration structure. Further, the bitmask and texture approach need to load vertex indices and texture coordinates in addition to the bitmask or texture. This data is listed in table 2 and plotted in figure 5 for increasing subdivision levels. Finally, the tree compression ratio in figure 5 is computed against the original opacity micromap data.
| Mode | Method | Sponza | Ecosys | New Sponza | San Miguel | Landscape |
|---|---|---|---|---|---|---|
| 2-State | Micromap | |||||
| Tree | ||||||
| Vulkan (FT/FB) | ||||||
| Bitmask | ||||||
| 4-State | Micromap | |||||
| Tree | ||||||
| Vulkan (FT/FB) | ||||||
| Bitmask | ||||||
| N/A | Texture | |||||
| N/A | Vertex Data | |||||
| N/A | Triangle Index | |||||
| N/A | Micromap/Tree Metadata |
 |
 |
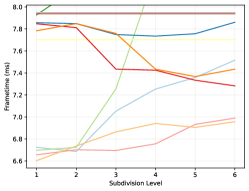
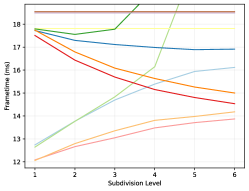
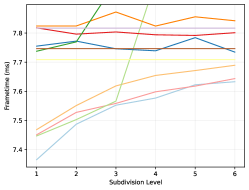
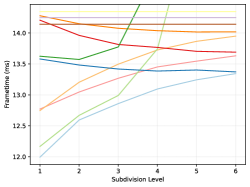
5.2. Runtime
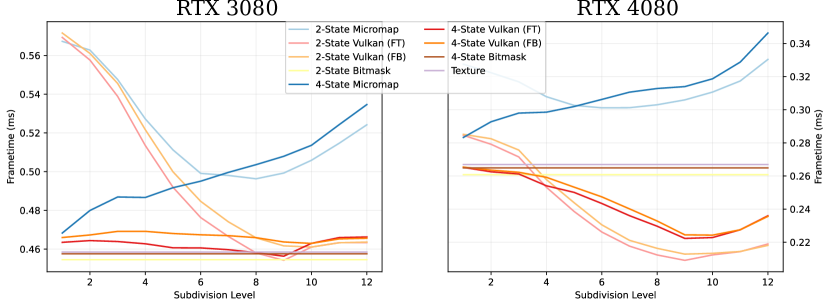
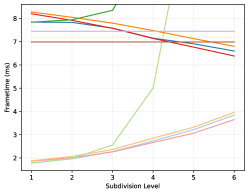
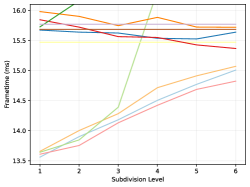
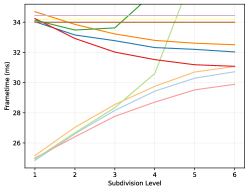
The frame rendertime is evaluated by implementing each method in an AnyHit shader, except for the Vulkan methods, as they cannot be controlled in such a fashion. All methods are rendered at with a refining ambient occlusion and stochastic transparency algorithm on an Nvidia RTX 3080 and 4080. Each sample time is gathered from the start- to end-of-pipe as reported by the Vulkan pipeline querying API. Note that the values presented in table 3 and figures 6, 7 and 8 represent the average over all viewpoints in a given scene weighted by the number of rendered frames. A per-pose breakdown is available in the supplemental material, however.
| Platform | Mode | Method | Sponza | Ecosys | New Sponza | San Miguel | Landscape |
|---|---|---|---|---|---|---|---|
| RTX 4080 | 2-State | Micromap | |||||
| Tree | |||||||
| Vulkan (FT) | |||||||
| Vulkan (FB) | |||||||
| Bitmask | |||||||
| 4-State | Micromap | ||||||
| Tree | |||||||
| Vulkan (FT) | |||||||
| Vulkan (FB) | |||||||
| Bitmask | |||||||
| N/A | Texture | ||||||
| RTX 3080 | 2-State | Micromap | |||||
| Tree | |||||||
| Vulkan (FT) | |||||||
| Vulkan (FB) | |||||||
| Bitmask | |||||||
| 4-State | Micromap | ||||||
| Tree | |||||||
| Vulkan (FT) | |||||||
| Vulkan (FB) | |||||||
| Bitmask | |||||||
| N/A | Texture |
| 2-State Renders | 4-State Render | ||||
|---|---|---|---|---|---|
| Sponza | Ecosys | New Sponza |
 |
 |
 |
| San Miguel | Landscape | Legend |
 |
 |
 |
| Sponza | Ecosys | New Sponza |
 |
 |
 |
| San Miguel | Landscape | Legend |
 |
 |
 |
6. Discussion
In this section we discuss the implications of our findings and attempt to interpret them.
6.1. Frame-time
Performance-wise, the first notable result is that there appear to be a small frametime improvement between a micromap created with the fast-build versus one with the fast-trace flag. However, the memory footprint is the same in both cases. Thus, it is likely that at this date the Nvidia driver only implement a single type of opacity micromap, but have a slightly more optimized access algorithm for the fast-trace case.
Further, even without official micromaps, we were able to detect a substantial improvement: Up to lower frame-time compared to using alpha masks directly. However, with only software emulation, we found a number of cases where using micromaps would instead increase the frame-time by up to . It seems as this is the primary case where the RTX 40-series significantly improve matters: Using the official micromap methods the worst recorded frame-time is only increased by and the best recorded one reduces it by . However, we also want to highlight the results from figure 6, which clearly shows a case where not using micromaps seems preferable if an RTX 40-series card is not available. However, we again want to note that the difference between all methods is very small: Only around .
Moreover, there appears to be only an extremely small improvement to using a bitmask instead of a real texture: Presumably the bandwidth cost from loading the vertex data offsets most of the potential gains. Then again, it would be interesting to see if compressing such a map similar to the approach suggested by (Fenney and Ozkan, 2023) would improve matters.
Lastly, accessing values from the tree compression is comparable to the other methods for micromaps of subdivision levels 3 or 4 as seen in figures 7 and 8. This also appears to be the more reasonable sizes for the scenes tested in this work, as can be seen among the micromap samples in the supplemental material. At higher levels however, it is arguably too slow to be of practical use, at least in its current form. This is likely caused by the bitscan function in algorithm 3: Each time the right-most child is accessed, all intervening subtrees for all other children must be scanned, the number of which roughly quadruples for each subdivision level. However, improvements to these types of data structures that use a bit more memory (about more) to ensure that the data can still be accessed in an efficient manner already exist (Gog et al., 2014). Investigating these options and finding a structure with a better trade-off seems like a worthwhile endeavor, and even if these structures cannot improve the access times, the tree structure would still be useful as a storage format, particularly for high subdivision levels.
6.2. Compression
The tree method presented in this work is able to compress the opacity micromap data extremely well: Typically down to between and of the original size, but in some extreme cases, such as for the New Sponza scene (2022) at subdivision levels, to less than the original size, or by times. A trend we expect to continue at higher subdivision levels.
However, while the compression is good in terms of memory footprint, the same is not necessarily true for the memory bandwidth. Similar to other compression methods such as Huffman coding (Huffman, 1952), a potentially large portion of memory may need to be decoded before the sought value is found, as is visualized in figure 9. This is also a notable deviation from the recommendations for texture compression given by (Beers et al., 1996) and the most important aspect that needs to be improved with a different succinct structure.
 |
6.2.1. Degenerate Cases
The tree compression algorithm seems to be good in the presented scenes, but there are a number of cases that cannot be compressed with this method. E.g., a micromap that always alternates between the micromap states will create a succinct tree that requires more memory than the original micromap, as depicted in figure 10. Such cases could be handled by extending the encoding to sub-trees rather than just leaf-nodes but as these cases are exceedingly rare in real content this may not be necessary in practice.
 |
 |
6.3. Comparing Micromaps to Textures
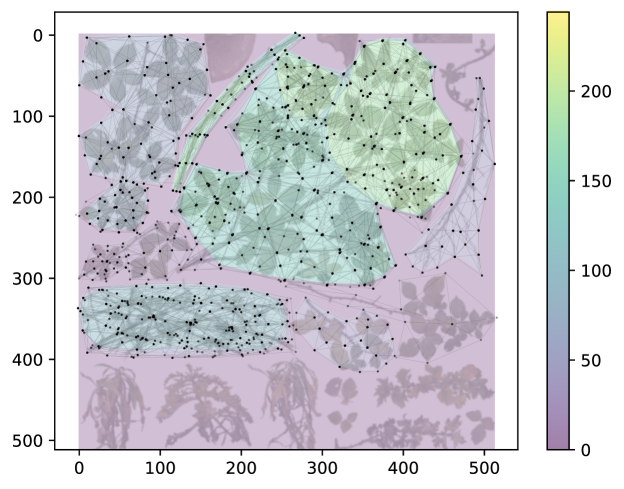
At first glance micromaps may appear to simply be a specialized kind of image texture. However, this is arguably not true, especially not for micromaps generated from alpha mapped foliage. Those kinds of micromaps are strongly tied to both the texture and the (uv) coordinates they were generated from. As such, they are more similar to the textures originally envisioned by (Catmull, 1974). Further, a cursory analysis of our chosen scenes quickly reveal that scenes that only use a single triangle or quad to represent foliage are exceedingly rare. As an example, figure 11 depicts a texture atlas from the CryTek Sponza scene (2011) with all unique triangle texture coordinates overlaid on top of it. This is a representative view of what can happen in practice:
-
•
In some cases, we have a well-structured grid of coordinates, in others,
-
•
we have many overlapping and crossing edges due to the coordinates being slightly misaligned.
In such cases, each triangle may create unique micromaps despite sharing a common texture and may consequently increase the acceleration structure bandwidth usage rather than reduce it.
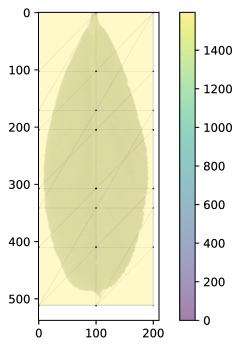
Further, in more modern scenes such as in San Miguel (2010) and Landscape (2016), leaves and branches are often modeled individually and split into many segments to allow artists to give them more depth as seen in figure 12. In these cases, micromaps work well, and relatively small subdivision levels can be used as only small parts of the mesh cover partially-transparent regions. However, in theses cases it is important to use the special triangle indices (see Section 3.1.2) to avoid having to explicitly represent all triangles, most of which will be fully-opaque.
 |
 |
7. Future Work
The micromap extensions are currently limited in scope but thanks to the extensible nature of the modern graphics APIs, it will be straight-forward to extend them in the future. The concept itself may even extend beyond these APIs:
The indexing algorithm (4) generalizes in multiple aspects: To other dimensions, shapes and subdivision levels. Investigating this further could lead to a number of interesting applications.
The tree accessing algorithm (3) only considered software implementations. As such, investigating the costs and benefits of these algorithms when implemented in hardware remains open, and while the presented version probably does not translate well into hardware, other uses of succinct data structures may be more amenable to this.
In regard to the extension itself: The current 2-state mode is limited to the fully-opaque or fully-transparent values. Adding one or more 1-bit modes to the opacity micromap extension that replace either of these values with the unknown-opaque or unknown-transparent could be an interesting way to further reduce the memory footprint. We plan to investigate the potential gains from such modes in the future.
Opacity micromaps is not the only available type: As mentioned in Section 3, displacement micromaps are already available on some hardware and other types are under development (Bickford, 2023). Some aspects of the presented tree encoding seem to extend to these types but more research is needed in this regard. Further, the algorithms presented in this paper only considered lossless encoding. Allowing lossy encoding of micromap values would open up many new avenues of research.
For the sake of brevity, the subject of constructing micromaps were not considered in this paper. Nvidia has published a framework for constructing them either during rendering or as a part of the asset preparation pipeline (GameWorks, 2022). Further, there is ongoing work to make similar tools available in Blender (Waldemarson, 2023). However, the aspect of how to create micromaps in an efficient and continuous manner is arguably still worth investigating.
Finally, the use-case for micromaps, and particularly opacity micromaps, is rather limited at the time of writing. Finding new and clever use-cases for them could be very interesting.
8. Conclusion
In this paper we introduced several novel algorithms related to the compression of micromaps by converting them to succinct 4-way trees, reducing their memory footprint by up to times in a number of representative scenes that use alpha mapped foliage extensively while remaining competitive at reasonable subdivision levels, but additional work is needed for this method to be practical in a high performance context.
Further, we have evaluated the potential performance gain from using the official Vulkan® and DirectX® opacity micromaps extension applied to alpha mapped geometry, confirming that the feature can provide an increase in frametime by at most when used in the so-called 4-state mode. Further, we have documented several important considerations regarding the use of 2-state micromaps that may be important for designers to be aware of. Moreover, we have introduced an alternative to the reference barycentric-to-index-algorithm that may be easier to understand.
Acknowledgements.
This work was partially supported by the Wallenberg AI, Autonomous Systems and Software Program (WASP) funded by the Knut and Alice Wallenberg Foundation. We would also like to thank Arm Sweden AB for letting Gustaf pursue a PhD as one of their employees. Additionally, we would like to thank Rikard Olajos, Simone Pellegrini and Mathieu Robart for their valuable input during this work. Finally, we are very grateful for the extensive input from our reviewers that helped us identify some areas that needed a bit of extra work.References
- Rendering from compressed textures. In Proceedings of the 23rd Annual Conference on Computer Graphics and Interactive Techniques, SIGGRAPH ’96, New York, NY, USA, pp. 373–378. External Links: ISBN 0897917464, Link, Document Cited by: §6.2.
- Nvidia Inc.. External Links: Link Cited by: §7.
- A subdivision algorithm for computer display of curved surfaces.. Ph.D. Thesis, The University of Utah, The University of Utah. Note: AAI7504786 Cited by: §6.3.
- Realistic modeling and rendering of plant ecosystems. In Proceedings of the 25th Annual Conference on Computer Graphics and Interactive Techniques, SIGGRAPH ’98, New York, NY, USA, pp. 275–286. External Links: ISBN 0897919998, Link, Document Cited by: Table 1.
- Compressed Opacity Maps for Ray Tracing. In High-Performance Graphics - Symposium Papers, J. Bikker and C. Gribble (Eds.), EUROGRAPHICS Association Groene Loper 3, 5612AE Eindhoven, pp. 23–31. External Links: ISSN 2079-8687, ISBN 978-3-03868-229-5, Document Cited by: §2, §6.1.
- CryTek sponza. Note: https://www.cryengine.com/asset-db/product/crytek/sponza-sample-scene Cited by: Table 1, Figure 11, §6.3.
- Nvidia Inc.. External Links: Link Cited by: §7.
- From theory to practice: plug and play with succinct data structures. In Experimental Algorithms, J. Gudmundsson and J. Katajainen (Eds.), Cham, pp. 326–337. External Links: ISBN 978-3-319-07959-2 Cited by: §6.1.
- Sub-triangle opacity masks for faster ray tracing of transparent objects. Proc. ACM Comput. Graph. Interact. Tech. 3 (2). External Links: Link, Document Cited by: Figure 2, §2, §2.
- A method for the construction of minimum-redundancy codes. Proceedings of the IRE 40 (9), pp. 1098–1101. External Links: Document, ISSN 2162-6634 Cited by: §6.2.
- Space-efficient static trees and graphs. In Proceedings of the 30th Annual Symposium on Foundations of Computer Science, SFCS ’89, USA, pp. 549–554. External Links: ISBN 0818619821, Link, Document Cited by: §3.2.
- Landscape. Note: https://www.laubwerk.com Cited by: Table 1, §6.3.
- The ACL2 home page. In http://www.cs.utexas.edu/users/moore/acl2/, Main Building (MAI) 110 Inner Campus Drive Austin, TX 78712, pp. 1. Cited by: §4.3.
- San miguel. Note: https://www.pbrt.org/scenes-v3/ Cited by: Figure 5, Table 1, §6.3.
- Micro-mesh construction. ACM Trans. Graph. 42 (4). External Links: ISSN 0730-0301, Link, Document Cited by: §2.
- Phenomenological transparency. IEEE Transactions of Visualization and Computer Graphics 23 (5), pp. 1465–1478. Note: IEEE Transactions of Visualization and Computer Graphics External Links: Link Cited by: §1.
- Intel sample library. Note: https://www.intel.com/content/www/us/en/developer/topic-technology/graphics-processing-research/samples.html Cited by: Figure 1, Figure 6, Table 1, §6.2.
- Nvidia. External Links: Link Cited by: §1.
- The Blender Foundation, Youtube. External Links: Link Cited by: §7.
- The Khronos Group Inc.. External Links: Link Cited by: §3.1, §4.3.
- The Khronos Group Inc.. External Links: Link Cited by: §1.
Appendix A Barycentric to Micromap Index Algorithm Details
The algorithm described in Section 4.3 works as follows:
-
(1)
Split the base triangle into 4 equal sized sub-triangles using the midpoint of each edge.
-
(2)
Then, using the vertex to edge mid-point relations;
and the typical formula for barycentric coordinates (), it is possible to derive the following relations to update the coordinates for each of the sub-triangles :
-
(3)
Note that the indexing and ordering of the updated coordinates are significant to handle rounding and winding changes for the top and middle triangles as the reference algorithm rounds globally away from the coordinate. Thus, the rounding direction has to be maintained as we recurse and change winding, requiring special handling for the top and middle triangles as follows:
-
•
Each time we recurse into the top triangle, flip the local index of the left and right subtriangles.
-
•
Each time we recurse into the middle triangle, round and tie-breaks to the middle rather than the right subtriangle.
See figures 13 and 2 for examples on how this works in practice.
-
•
![[Uncaptioned image]](/images/succinct-opacity-micromaps/x67.png)
![[Uncaptioned image]](/images/succinct-opacity-micromaps/x68.png)
![[Uncaptioned image]](/images/succinct-opacity-micromaps/x69.png)
![[Uncaptioned image]](/images/succinct-opacity-micromaps/x70.png)
![[Uncaptioned image]](/images/succinct-opacity-micromaps/x71.png)