Parallel Axis Split Tasks for Bounding Volume Construction with OpenMP^®

Abstract

Many algorithms in computer graphics make use of acceleration structures such as Bounding Volume Hierarchies (BVHs) to speed up performance critical tasks, such as collision detection or ray-tracing. However, while the typical algorithms for constructing BVHs are relatively simple, actually implementing them for performance critical systems is still challenging. Further, to construct them as quickly as possible, it is also desirable to parallelize the process. To that end, parallelization APIs such as OpenMP^® can be leveraged to greatly simplify this matter. However, BVH construction is not a trivially parallelizable problem. Thus, in this paper we propose a method of using OpenMP^® tasking to further parallelize the spatial splitting algorithm and thus improve construction performance. We evaluate the proposed way and compare it with other ways of using OpenMP^®, finding that some of these work well to improve the construction time by between 3 and 5 times on an 8-core machine with a minimal amount of work and negligible quality reduction of the final BVH.

1 INTRODUCTION

Bounding volume hierarchies are arguably one of the most important data-structures currently in widespread use in the field of computer graphics, and it is often prominently used for ray-tracing during image synthesis. However, it is also used for various other tasks, such as collision detection or occlusion based audio mixing [6]. As such, it is often important to be able to create these hierarchies with as high quality as possible, thus ensuring that when the structure is used to accelerate some task, that query operation is as fast as possible.

Typically, the recursive algorithms used to build these structures are relatively simple, but rewriting them for maximum throughput in a parallelized context can be challenging. Thus, modern versions of parallelization APIs such as OpenACC or OpenMP^® [5] can be leveraged to trial various paralellization strategies before committing to a particular approach, or in other cases, be used directly in the original algorithm. However, there are often multiple ways to apply these APIs. As such, finding the most performant way to use them can be a beneficial endeavor.

2 RELATED WORK

Over the years, many variations of acceleration structures have been invented, notable examples being octrees [14], kd-trees [4] and bounding volume hierarchies, or BVHs. Lately however, BVHs have become the more popular category for four main reasons: They have a predictable memory footprint, queries are robust and efficient, they easily adapt to dynamic geometry, and most crucially: The build itself is scalable; allowing users to either quickly create a hierarchy with possibly slow queries, or, to spend more time upfront to yield potentially faster ones [16].

Thus, as it is assumed that construction of an optimal BVH is an NP-hard problem [11], numerous heuristics and algorithms have been developed for generating these hierarchies, and depending on the target application, one of the above approaches are typically preferred:

1. For interactive applications, such as real-time ray-tracing, fast builders running on the GPU are pre-dominantly used, such as the LBVH [12], HLBVH [17], and more recently, the H-PLOC algorithm by [3].

2. For offline ray-tracing applications, such as those described by [18], slower builders, such the SBVH [19] or PRBVH [15] may be preferable, where any improvement in the quality of the BVH is often recovered during the actual ray-tracing phase [1].

No matter the application however, it is always desirable to be able to create these structures as quickly as possible. To that end, these build processes are usually parallelized as much as possible. Fast builders typically do this by relaxing some spatial constraints to expose more parallelism, making them amenable to fast GPU implementations. In contrast, quality focused builders typically create their hierarchies with a CPU implementation, as that often provides a bit more flexibility when analyzing the input geometry [8, 21]. However, many of these algorithms build the hierarchy from the top-down, thus initially suffering from poor scaling in the first few splitting tasks. To that end, a number of parallelization schemes have been proposed to extract additional parallelism from these early splits [22, 23, 7]. These approaches typically attempt to split up the computations over all primitives, thus providing a large amount of potential parallelism, but requires a number of complex synchronization mechanisms to function. In contrast, in this paper we propose an arguably simpler approach by only parallelizing over the split axes, thus losing some opportunities for parallelization, but in turn only requiring a relatively simple synchronization method.

3 BACKGROUND

This section provides relevant background information about the SBVH algorithm [19] targeted for parallelization with OpenMP^® in this work.

3.1 Spatial Split BVH

While BVHs have many great qualities, they can perform poorly in scenes with many overlapping primitives, as is often the case with triangle meshes. In those cases, Kd-trees [4] are typically able to achieve higher ray-tracing performance. To that end, [19] developed a variation of the BVH construction algorithm that drew inspiration from the spatial splits used by kd-trees, thus creating one of the highest performing triangle based BVH algorithms in terms of query-time, which is typically referred to as the SBVH algorithm. However, while the query-times are fast, its major drawback is the construction time: It is typically the slowest BVH construction algorithm in widespread use. Furthermore, this algorithm is challenging to parallelize, as part of its operation depend on being able to dynamically create new references to triangles with subdivided bounding boxes.

This particular aspect was improved by [9], who noted that only around $10\mathrm{\%}$ extra references are needed in most scenes. Thus, by pre-allocating memory for these and distributing them in each split task, parallelization gets a bit easier. Thus, in this paper we further simplify this matter, showing how the SBVH algorithm can be easily parallelized with the help of OpenMP^®.

3.2 OpenACC and OpenMP^®

Figure 1: Graphical visualization of the typical OpenMP^® usage for splitting up tasks into parallel regions.

OpenACC and OpenMP^® are APIs for performing numerous types of multi-processing tasks in a convenient and portable fashion in the C, C++ and Fortran programming languages through the use of compiler directives and library routines. Both of these are managed by non-profit organizations: The OpenMP Architecture Review Board, and the OpenACC organization, jointly governed by all major compiler and hardware developers with collaboration from their user communities.

As illustrated in figure 1, these APIs provide a relatively simple way of successively parallelizing portions of a program, and the simplest application of it is typically through the use of the parallel for compiler pragma from the OpenMP^® API, as shown in figure 2.

⬇

size_t n = 8;

#pragma omp parallel for num_threads(n)

for (size_t i = 0; i < height; ++i)

{

for (size_t j = 0; j < width; ++j)

{

im[i][j] = ray_trace(i, j);

}

}

Figure 2: A simple for-loop parallelized using an OpenMP^®compiler directive.

OpenMP^® 3.0 and onwards also enables the manual creation of parallel tasks that may be submitted to a thread-pool, a process typically referred to as tasking. Further, tasks may even recursively create more tasks, as seen in figure 3, thus enabling complex algorithms to be parallelized in simple fashion [2]. However, some care is still needed to ensure that each task is able to perform a suitable amount of work to account for the overhead of its creation. Beyond this, OpenMP^® also provide directives for automatically converting the iterations of loops to tasks with the taskloop directive and even performing guided SIMD vectorization of loops.

In contrast, OpenACC was originally intended for offloading tasks to discrete accelerator devices, thus providing a simple interface to program coprocessors such as GPUs. However, modern versions of this API can also parallelize on the host CPU when required. Additionally, as of OpenMP^®4.0, similar device offloading capabilities are available for that API as well, even if the performance of these features may be a bit worse [20].

Still, applying device offloading correctly often requires significantly more effort to ensure that the data can be transferred correctly to the coprocessor, often forcing a major restructuring of the original algorithms. As such, these types of approaches are out of scope for this paper.

⬇

int fibonacci(int n)

{

int fn1, fn2;

if (n == 0 || n == 1)

return n;

#pragma omp task shared(fn1)

fn1 = fibonacci(n - 1);

#pragma omp task shared(fn2)

fn2 = fibonacci(n - 2);

#pragma omp taskwait

return fn1 + fn2;

}

Figure 3: A more complex parallelization example to demonstrate the use of OpenMP^® tasking. Note that, while illustrative, this particular example would likely not benefit much from parallelization as the overhead of creating tasks likely outweigh the cost of the work itself.

4 ALGORITHM

This section provides a high-level overview of how the SBVH algorithm recursively constructs a hierarchy from a collection of primitive references, i.e., a set of triangles with potentially subdivided bounding boxes. Our contribution for parallelizing this algorithm with OpenMP^® is also described here.

Fn build(references, bounds):

      if create leaf? then

            return;

       end if

       $obj\leftarrow \text{object\_split(}\text{references, bounds}\text{)}$;

       $spt\leftarrow \text{spatial\_split(}\text{references, bounds}\text{)}$;

       if $spt.cost\le obj.cost$ then

            perform spatial split;

      else

            perform object split;

       end if

      (1)build(left-references, left-bounds);

      (2) build(right-references, right-bounds);

      

EndFn

Algorithm 1 High-level overview of the SBVH construction algorithm. The functions object_split and spatial_split are described in algorithms 2 and 3 respectively. Further, lines that may be parallelized with tasks are marked with 1 and 1 as is described in section 4.2.

Fn object_split(references, bounds):

      (3) foreach axis do

            sort references;

             foreach reference do

                  estimate split cost;

                  

             end foreach

            

       end foreach

      return optimal split cost and location;

      

EndFn

Algorithm 2 High level overview of the BVH object split estimation: Find the appropriate splitting axis and segment the objects to the left and right side of it. Note that the axis-loop on line 2 may be parallelized as described in section 4.2.

Fn spatial_split(references, bounds):

      (4) foreach axis do

            foreach reference do

                  chop references into bins;

                   split references on bin boundaries;

                  

             end foreach

            find axis splitting plane;

            

       end foreach

      return optimal split axis and plane;

      

EndFn

Algorithm 3 High level overview of the BVH spatial split estimation: Find the appropriate splitting axis and plane, and segment or create references to the left and right side of it. Note that the axis-loop on line 3 may be parallelized as described in section 4.2.

4.1 SBVH Splitting Tasks

In algorithm 1 each SBVH splitting task can recursively create two more work-packets up to the point that it decides to create a leaf-node instead, in a fashion that is very similar to the OpenMP^® tasking example in figure 3. This also means that the algorithm is not able to run at full capacity until enough tasks have been spawned to keep all available threads occupied. To that end, we propose that further subdividing the splitting task itself may expose more beneficial parallelism during the early stages of the SBVH construction. E.g., by creating tasks for searching each splitting plane along each of the primary axes marked in algorithms 2 and 3, and visualized in figure 4. Further, this may allow more expensive splitting heuristics to be evaluated each time, as more of them can be tried in parallel. E.g., more bins can be used for the binned surface area heuristic (SAH) by [22], or a different, more expensive heuristics such as the original SAH variant proposed by [10, 13] can be used. This could theoretically improve the BVH quality, while still providing some balance between the amount of work being done and the time it takes to execute each task.

Figure 4: Graphical representation of the task creation process during the construction of an SBVH as well as the further parallelizable regions of a single BVH splitting task.

4.2 Variants

In order to evaluate the potential SBVH build time improvement from multithreading with various OpenMP^® constructs, we apply one or more source level patches to a base implementation of the algorithm; effectively inserting the necessary compiler directives (i.e., #pragma omp …) at the correct locations. In total, we evaluate five different variants of this approach:

NoOpenMP

Reference implementation without any OpenMP^® directives.

TaskingOnly

Parallel tasks are created using the #pragma omp task directive for each recursive call to build in algorithm 1, similar to the tasking example in figure 3.

Tasks

Same as TaskingOnly, but create additional tasks for each iteration of the object and spatial axis search loops, i.e., for the marked loops in algorithms 2 and 3 and ensure that these tasks are synchronized afterwards using the #pragma omp taskwait directive.

Taskloop

Same as Tasks, but use the #pragma omp taskloop directive instead, thus avoiding the need for explicit task synchronization through the #pragma omp taskwait directive.

ParallelFor

Same as TaskingOnly, but use nested parallelism for each object and spatial axis search using the #pragma omp parallel for directive, similar to the example in figure 2.

Further, we also investigate only parallelizing the object and spatial split search tasks, i.e., we do not parallelize the recursive splits in algorithm 1. However, these variants are not expected to scale beyond three available threads as there are only three axes to search in each task. To that end, we test the following additional variants:

NoTaskingFor

Use the #pragma omp parallel for directive to search each axis, as in the ParallelFor variant.

NoTaskingTasks

Same as NoTaskingFor, but use OpenMP^® task constructs as in the Tasks variant.

NoTaskingTaskloop

Same as NoTaskingTasks, but use the #pragma omp taskloop directive instead, same as for the Taskloop variant.

5 RESULTS

All BVH construction algorithms and their variations ran on an Intel(R) Core(TM) i7-6700K CPU @ 4.00GHz built by the gcc (gcc (Ubuntu 11.4.0-1ubuntu1 22.04) 11.4.0 ) and clang (Ubuntu clang version 14.0.0-1ubuntu1.1 ) compilers.

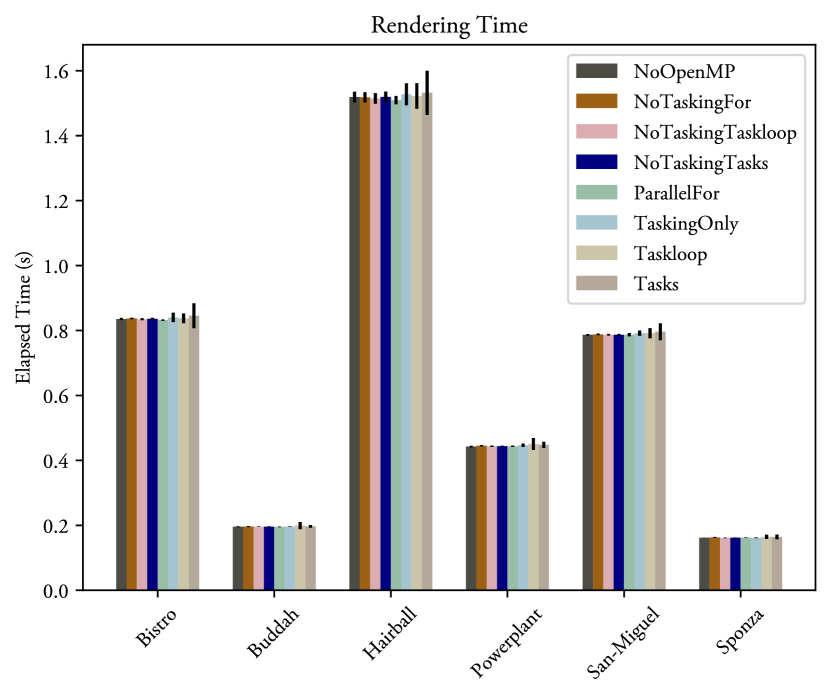
Each scene was rendered with an OpenCL based ray-tracer running on an NVIDIA GeForce RTX 3060 GPU using an ambient occlusion algorithm, example renders of which can be seen in figure 5.

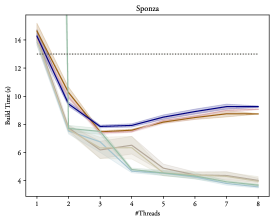
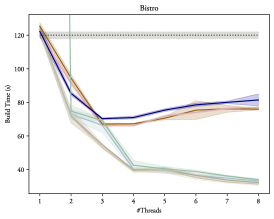
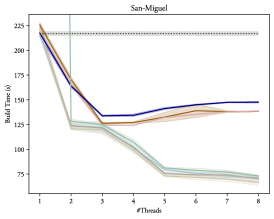
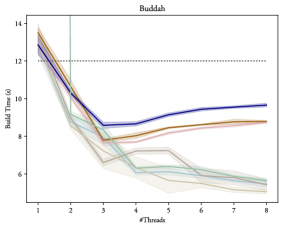
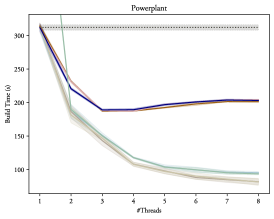
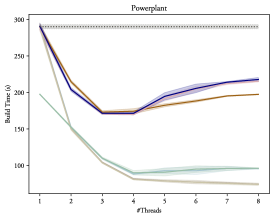
The results depicting how these variants scale with additional threads can be found in figures 6 and 7 for gcc and clang respectively, clearly demonstrating that OpenMP^® is able to provide a substantial improvement to the BVH construction time: Up to 5 times faster than the single thread result on our 8-core setup. Thus, proving that the additional task parallelization of the object and spatial axis searches proposed in section 4.1 is able to provide some additional benefits. However, there is only a non-significant difference between using plain tasks (Tasks and NoTaskingTasks) or using the taskloop directive (Taskloop and NoTaskingTaskloop), as such, performance-wise, it does not matter which of these are actually used, but the taskloop directive is usually a bit easier to read at a glance and does not require explicit synchronization, and may thus be preferred.

Sponza: $393\mathrm{m}$eshes, $\mathrm{262\hspace{0.17em}267}\mathrm{t}$riangles.	Hairball: $2\mathrm{m}$eshes, $\mathrm{2\hspace{0.17em}880\hspace{0.17em}002}\mathrm{t}$riangles.	Bistro: $1\mathrm{m}$esh, $\mathrm{3\hspace{0.17em}847\hspace{0.17em}246}\mathrm{t}$riangles.
San-Miguel: $287\mathrm{m}$eshes, $\mathrm{9\hspace{0.17em}980\hspace{0.17em}699}\mathrm{t}$riangles.	Buddah: $1\mathrm{m}$esh, $\mathrm{1\hspace{0.17em}087\hspace{0.17em}720}\mathrm{t}$riangles.	Powerplant: $21\mathrm{m}$eshes, $\mathrm{12\hspace{0.17em}759\hspace{0.17em}246}\mathrm{t}$riangles.

Figure 5: The scenes investigated during this work along with their mesh and triangle counts.

Figure 6: Visualization of how each variant scales with more available threads in the gcc implementation.

Figure 7: Visualization of how each variant scales with more available threads in the clang implementation.

6 DISCUSSION

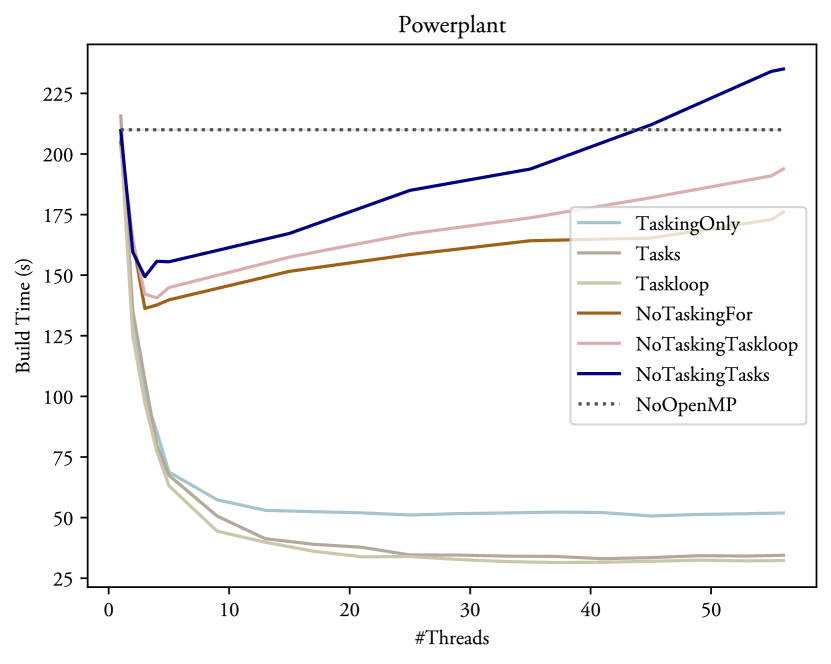
While figures 6 and 7 demonstrate a notable improvement, it is also evident that the scaling is logarithmic: Each additional thread is able to increase the performance, but each subsequent gain is always diminished. In fact, as can be seen in figure 8, on a heavily multi-threaded machine scaling almost completely stops between 10 and 20 threads. This can be explained by viewing this type of BVH construction as a divide-and-conquer problem: At first, each additional thread greatly reduces the amount of necessary work, but eventually each task becomes too small to benefit from being processed in parallel, thus stopping the scaling.

Figure 8: Scaling results for the Powerplant scene on a heavily multithreaded machine (Intel(R) Xeon(R) w7-3465X ).

Furthermore, depending on how the SBVH algorithm is implemented, some synchronization, or critical regions may be necessary. As an example, in our implementation, one such region is used to allocate indices for each of the BVH nodes. Thus, one side effect of the parallelization is that the ordering of the nodes is no longer guaranteed to be deterministic. This is particularly noticeable for the Tasks and Taskloop variants that may interleave axis searches between the main build tasks. While subtle, this effect is evident in figure 9 where it manifests as a minor increase in the average and variation of the rendering time due to cache-misses from the increased memory fragmentation of the BVH nodes.

Figure 9: Rendering time using the constructed BVH by each of the OpenMP constructs using a OpenCL based ray-tracer.

Further, it appears that there is a moderate gain from only parallelizing the object and spatial split axis searches, with a minor lead for the NoTaskingFor variant, which is likely explained by the parallel for directive being more mature and that it has less overhead than a task queue implementation. Thus, this method may be beneficial if there is a strict requirement on a deterministic BVH hierarchy. As expected, none of these approaches scale beyond three threads, and should in fact be locked to that level, as the more threads cause a significant performance overhead.

Additionally, in figure 7, we can see that when using the clang compiler, it works well to create nested parallel regions, i.e., when tasks and parallel for are used inside one-another, as is done in the ParallelFor variant. In contrast, the gcc implementations in figure 6 experience dramatic regressions by several times the baseline for this variant. This is most likely a consequence of the thread-cache not being used for nested parallel regions. Thus, given that the performance is in-line with the Tasks and Taskloop variants, it may be prudent to avoid nested regions, unless the targeted compiler is known beforehand.

Finally, note that using OpenMP^® is not strictly beneficial: If the code is serialized, i.e., only a single thread is being used, effectively all variants have a small but noteworthy penalty to the construction times.

7 FUTURE WORK

Figure 10: A potentially improved SBVH construction task: The object and spatial cost evaluation are theoretically independent and may thus run in parallel. Further, by determining if a child node would become a leaf before recursing can greatly reduce the number of necessary tasks.

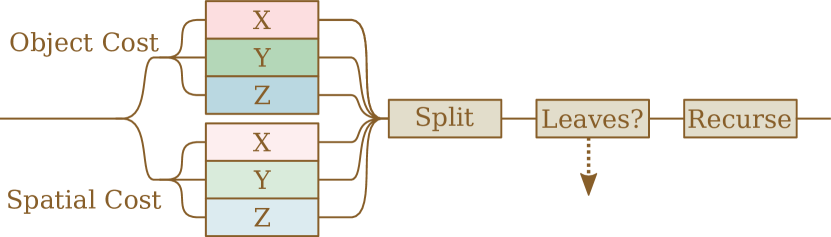
Implementation-wise, there are a number of things that could be improved: Currently, the additional tasks for the axis searches are beneficial, particularly when each split contains a lot of primitives. However, smaller tasks are typically less useful, but OpenMP^® also has support for conditionally merging or spawning tasks. Thus, finding an appropriate metric that can be used for tuning the task creation process may be a beneficial endeavor. Moreover, as seen in figure 10, it should be possible to restructure the splitting task itself to expose more opportunities for parallelism and thus improve the performance even further. Additionally, this work only considered binary BVHs, but research is currently being done on hierarchies with higher branching factors. While building such structures is more complicated, the additional branching may provide even more opportunities to parallelize the construction.

As noted in section 3.2, modern implementations of OpenMP^® and OpenACC have support for offloading computations to coprocessors using e.g., the target directive. This was not investigated as a part of this work due to the additional complexity of mapping the input data-structures to the devices. Furthermore, as can be seen in figure 8, this particular algorithm does not appear to scale beyond 30 or 40 threads, thus it is questionable whether it would benefit from a massively parallel architecture.

8 CONCLUSIONS

OpenMP^® is a very convenient way to drastically reduce the amount of necessary code required to implement many complex algorithms, such as the construction of bounding volume hierarchies (BVHs). In this paper we have both devised a new way of further parallelizing the splitting tasks of the so-called Spatial Split BVH algorithm, and tested numerous ways of applying OpenMP^® on it. Thus showing that OpenMP^® tasking can be effectively leveraged to keep the construction algorithms simple while still improving the build time by up to 5 times on a modern 8-core consumer workstation.